LATEST

NASA's Near Space Network enables the PACE Climate...
Wed, Apr 17th 2024NASA's PACE mission achieved a significant...
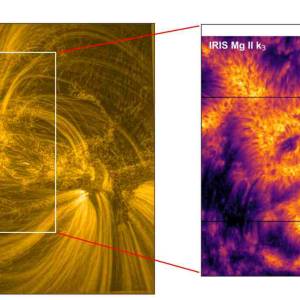
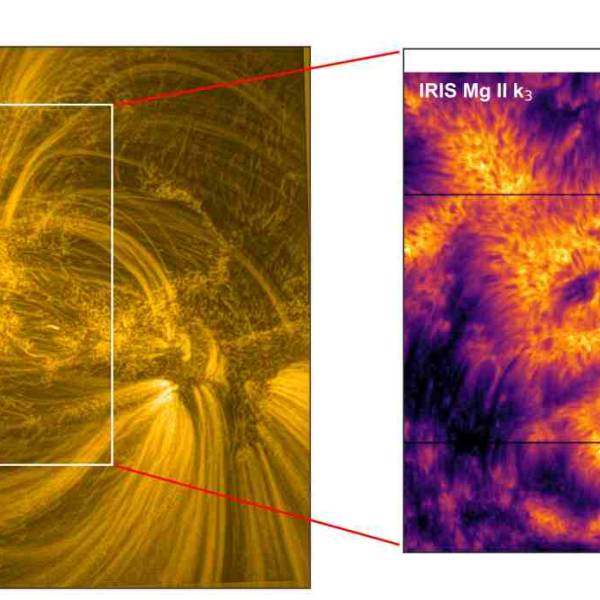
Scientists utilize supercomputer simulations to...
Wed, Apr 17th 2024Cutting-edge research and supercomputer...
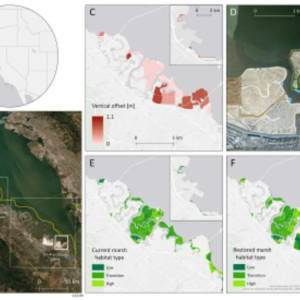
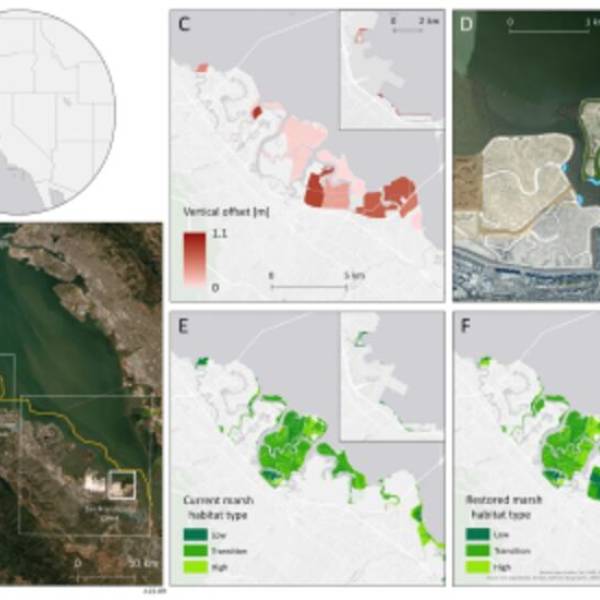
Salt marsh restoration study reveals promising...
Thu, Apr 11th 2024Supercomputer simulations demonstrate the...

Marbell leads Woolpert's geospatial business...
Wed, Apr 10th 2024Woolpert, a national architecture, engineering,...
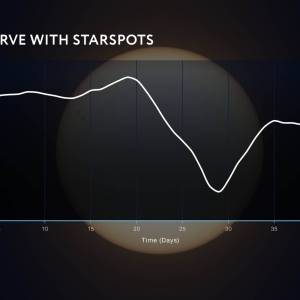
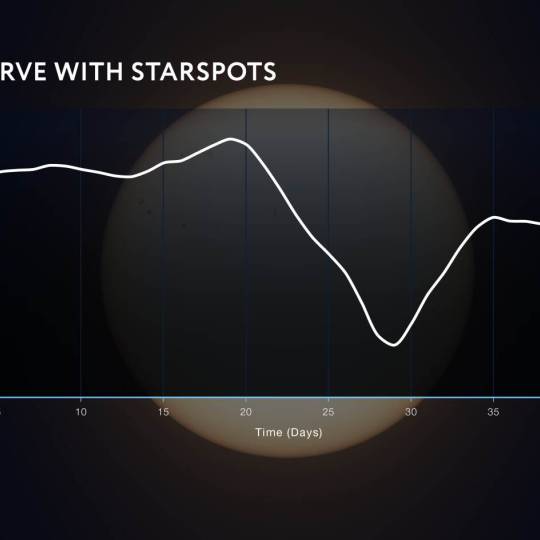
NASA's Roman Telescope uses Convolutional Neural...
Thu, Apr 4th 2024Determining the age of stars has been a...

Australia on track for unprecedented, decades-long...
Wed, Apr 3rd 2024The Australian National University (ANU) and the...
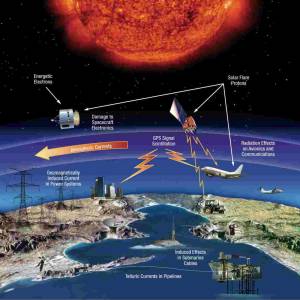
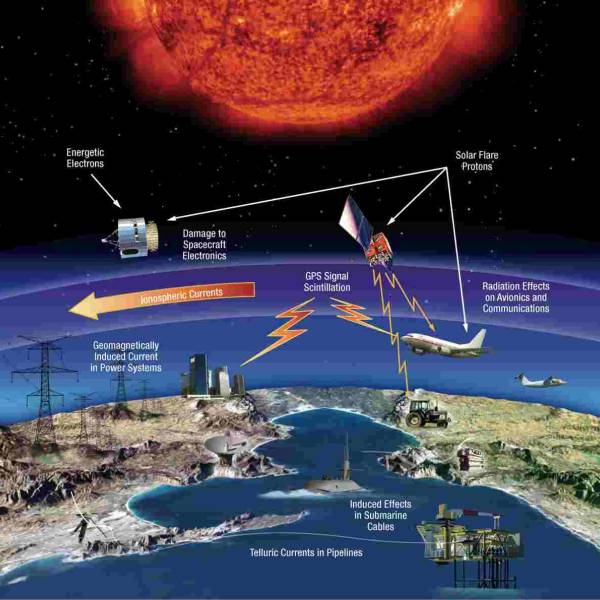
NASA predicts the Sun's corona behavior, revealing...
Tue, Apr 2nd 2024Scientists at Predictive Science are conducting a...

Revolutionizing precision agriculture: The impact...
Tue, Apr 2nd 2024The Spanish researchers in Hydraulics and...
Artificial intelligence chatbot outperforms...
Mon, Apr 1st 2024In an era of rapid technological advancements, the...