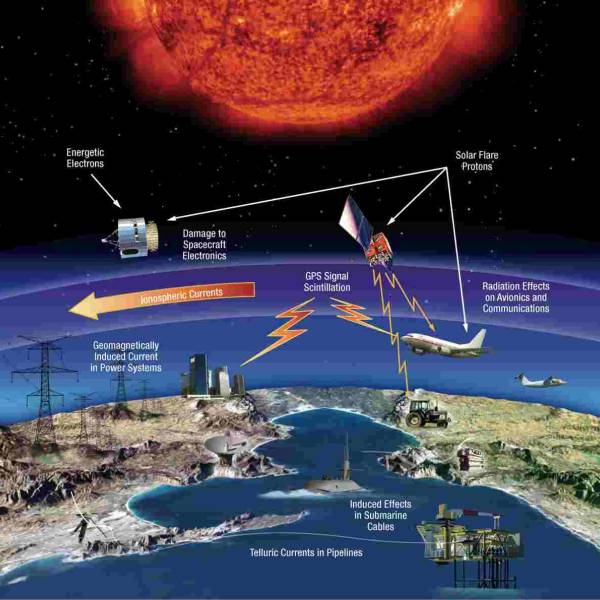
LATEST
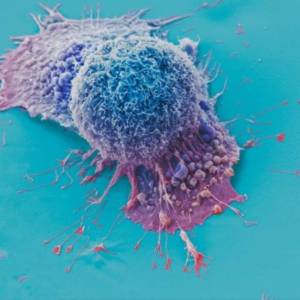
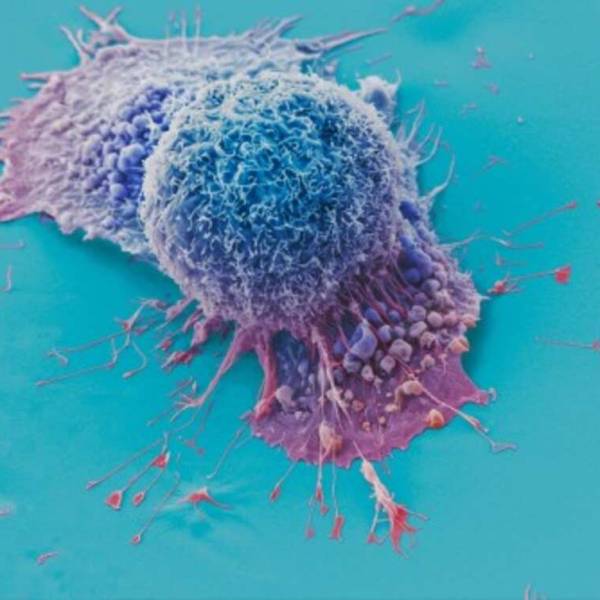
AI tool predicts responses to cancer therapy using...
Thu, Apr 18th 2024A recent study conducted by researchers from...

NASA's Near Space Network enables the PACE Climate...
Wed, Apr 17th 2024NASA's PACE mission achieved a significant...
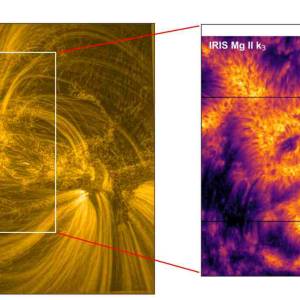
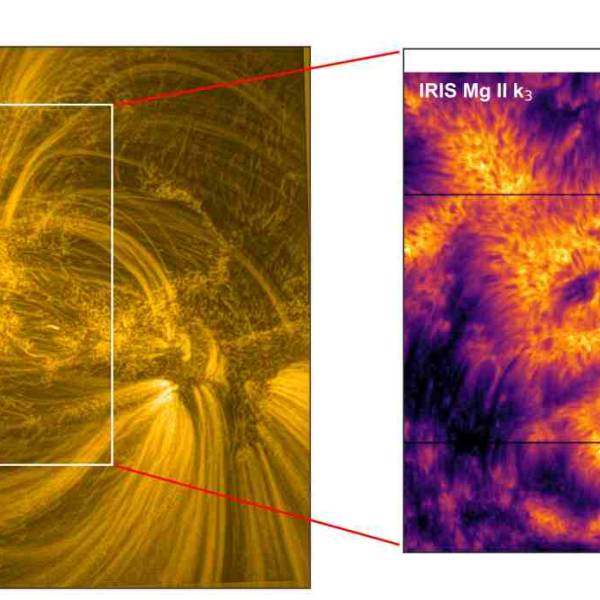
Scientists utilize supercomputer simulations to...
Wed, Apr 17th 2024Cutting-edge research and supercomputer...
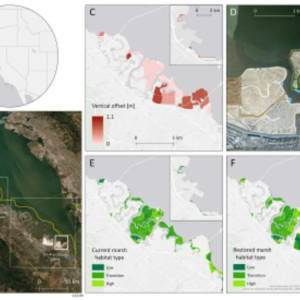
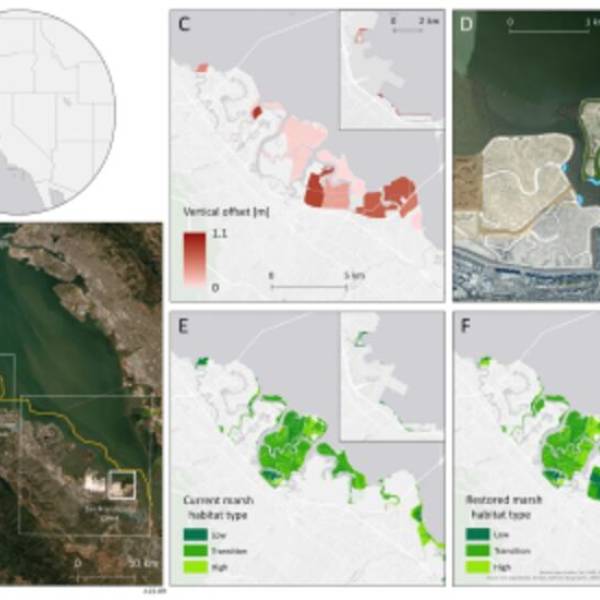
Salt marsh restoration study reveals promising...
Thu, Apr 11th 2024Supercomputer simulations demonstrate the...

Marbell leads Woolpert's geospatial business...
Wed, Apr 10th 2024Woolpert, a national architecture, engineering,...