THE LATEST

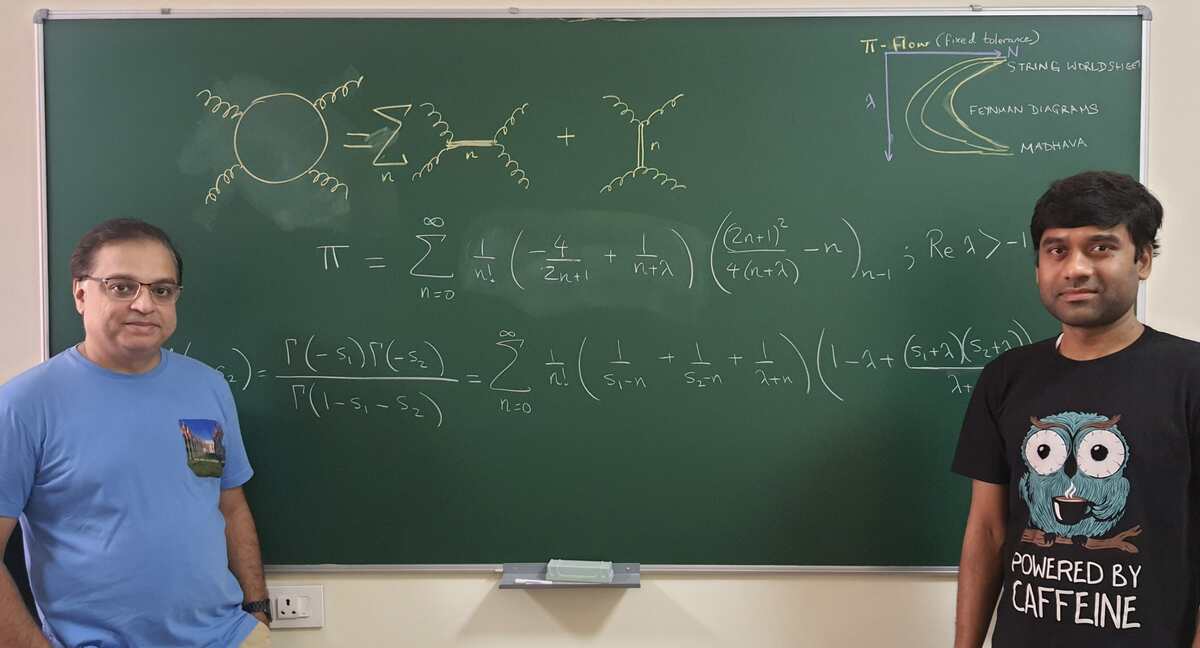
A team of scientists at the Indian Institute of Science (IISc) has achieved a breakthrough in the fields of physics and mathematics by discovering a new series representation for the irrational number π, also known as pi. The research, conducted within the realm of string theory, has introduced a novel approach for deriving pi from calculations related to complex processes like quantum scattering of high-energy particles.

Led by post-doctoral researcher Arnab Saha and Professor Aninda Sinha from the Center for High Energy Physics (CHEP) at IISc, the study has resulted in the formulation of a unique formula that closely approximates the historically significant series for pi put forward by Indian mathematician Sangamagrama Madhava in the 15th century. This marks the first-ever series for pi recorded in history.

Sinha explains, "Our initial focus was not specifically on uncovering a new perspective on pi. Instead, our efforts were concentrated on delving into high-energy physics within the domain of quantum theory, to develop a model with refined parameters to understand particle interactions. The discovery of a new method for interpreting pi naturally emerged from this pursuit."

The research team's specialization in string theory, a theoretical framework proposing that all quantum processes in nature originate from various modes of vibrations on a string, primarily revolves around the interactions of high-energy particles. The study aims to unravel the complexities of understanding particle interactions by employing minimal and straightforward factors. This approach falls under the purview of "optimization problems," which involves modeling intricate processes while considering numerous parameters for each moving particle, including factors such as mass, vibrations, and degrees of freedom relevant to its movement.

Saha, who has been actively engaged in addressing the optimization problem, sought to establish an efficient model for representing these particle interactions. As part of this endeavor, he collaborated with Sinha to combine two mathematical tools—an Euler-Beta Function and the Feynman Diagram—to develop an efficient model. Euler-Beta functions, widely used to solve problems in various branches of physics and engineering, including machine learning, were integrated with the Feynman Diagram, a mathematical representation explaining energy exchange during particle interactions and scattering.

The integration of these mathematical tools has not only resulted in an efficient model that illuminates particle interactions but has also led to an innovative series representation of pi. In mathematics, a series is used to represent a parameter such as pi in its fundamental form. Sinha explains, "Finding the correct number and combination of parameters to rapidly approach the exact value of pi has long presented a challenge. The series discovered by our team combines specific parameters in a manner that enables rapid attainment of the value of pi, which can then be incorporated into calculations relating to the deciphering of high-energy particle scattering."

The implications of these findings are profound, as they have opened up new avenues for advancing our understanding of complex mathematical and physical phenomena. Sinha highlights that while the practical applications of these theoretical findings are not yet fully realized, historical precedents—such as Paul Dirac's groundbreaking work in 1928, which ultimately led to the design of Positron Emission Tomography (PET)—underscore the potential for unforeseen practical applications arising from fundamental theoretical research.

The research, while currently theoretical, represents a significant milestone in the fields of mathematical and theoretical physics. As indicated by Sinha, "Engaging in such research, despite its potential non-immediate practical applications, offers the pure pleasure of engaging in theory for the sake of advancing the frontiers of scientific knowledge."