MOVIES

The RIKEN Nishina Center for Accelerator-Based Science (RNC) was named after Yoshio Nishina, the father of atomic physics in Japan and RIKEN’s fourth director. At the RNC’s Quantum Hadron Physics Laboratory, Tetsuo Hatsuda and other researchers are using supercomputers to further the work of Nobel Prize-winning theorists Hideki Yukawa and Sin-Itiro Tomonaga, who worked in Nishina’s laboratory at RIKEN while pioneering research into electrons and atomic nuclei.

Calculating the magnetic forces of the electron

The basis of some of the questions being explored using RIKEN’s supercomputers can be traced to the late 1940s when Tomonaga, along with Richard Feynman, Julian Schwinger and others, established the discipline of quantum electrodynamics (QED), which is the quantum field theory of photons and charged particles, and forms a fundamental thread running through the Standard Model of modern physics. Many students at the University of Tokyo at the time—including Toichiro Kinoshita, now professor emeritus at Cornell University in the United States and visiting researcher at the Quantum Hadron Physics Laboratory—participated in a seminar by Tomonaga, then a professor at Tokyo Bunrika University (presently the University of Tsukuba).

“In those days, I was studying physics under the tutelage of Kunihiko Kodaira (a recipient of the Fields Medal for mathematics in 1954), who was the only researcher of quantum field theory at the University of Tokyo,” says Kinoshita, in retrospect. “However, since Kodaira specialized in mathematics, University of Tokyo students who wanted to learn about quantum field theory rushed to Tomonaga’s laboratory instead. Yoichiro Nambu (the 2008 Nobel Laureate in Physics) was among them.”

In 1952, Kinoshita and Nambu joined the Institute for Advanced Study in the United States. They subsequently engaged in many years of research at the University of Chicago and Cornell University, respectively. In 1966, Kinoshita spent a year working at CERN (the European Organization for Nuclear Research) in Switzerland where he was astonished by their experimental data on muons.

Muons, like electrons, are fundamental particles and possess both charge and magnetic properties. The g-factor is a measure of the magnetic forces of these particles (known as the magnetic moment), and in quantum mechanics has the value of the integer 2, as calculated by the Dirac equation. However, in 1947, US physicist Polykarp Kusch (recipient of the 1955 Nobel Prize in Physics) showed experimentally that the value of the g-factor is not precisely 2, but instead deviates by about 0.1%. In 1948, Schwinger demonstrated using QED calculations that this phenomenon is caused by electrons and muons emitting and reabsorbing a photon—a particle that transmits light. While at CERN, Kinoshita saw experimental data corresponding to high-precision measurements of the muon g-factor.

“The best way of determining the accuracy of QED is to examine the g-factor value. This is because we can determine the g-factor at high precision both experimentally and theoretically as it represents a simple system involving the nature of a single particle,” explains Kinoshita.

The deviation of the g-factor away from 2 is most influenced by the emission and reabsorption of one photon. Emission and reabsorption of photons can be visually represented by a Feynman diagram (Fig. 1, part A, inset). For electrons, a single Feynman diagram can depict the case for one photon, allowing the g-factor to be calculated manually. To obtain the g-factor value to a higher level of precision, it is necessary to determine how the g-factor is influenced when the number of photons to be emitted and reabsorbed increases to 2 or 3. For 2 photons, 7 different Feynman diagrams are available and the g-factor may still be manually calculated. However, with 3 photons, 72 different Feynman diagrams exist, making manual calculation quite difficult.

To obtain the g-factor value of the muon at the precision of the experimental data from CERN, it was necessary to calculate the influence of up to 3 photons. Therefore, Kinoshita began to derive the g-factor through QED-based large-scale computation. In 1974, he succeeded in determining the g-factor value of the electron to the precision of 1 part in 3 billion.

Kinoshita assumed that this research was finally complete, but soon learned that researchers at the University of Washington had begun new experiments to measure the electron’s g-factor. “[The researchers] were seeking to obtain measurements to the level of precision of 1 part in 100 billion—three digits greater than the precision of conventional experiments. So I could not help but continue my research.”

Understanding ultimate theories with QED

To further increase the precision of his measurements, Kinoshita began to determine the influence of 4 photons. This required the calculation of 891 different Feynman diagrams. “I created a prototype method for large-scale computation when I was attempting to calculate the influence of 3 photons. I then began to use an expanded version of this prototype in my calculations,” says Kinoshita. “When the computing process reached its final stage, I asked Makiko Nio, who had been a student at my laboratory at Cornell, to join the project.”

In 2007, Kinoshita, Nio and colleagues succeeded in calculating the influence of 4 photons and deriving the g-factor value of the electron to the precision of 1 part in 1 trillion. However, the following year, researchers at Harvard University announced that they had obtained measurements to the precision of 1 part in 3.6 trillion. So, to increase the precision of Kinoshita’s calculations even further, 12,672 different Feynman diagrams representing the influence of 5 photons had to be computed (Fig. 1, part A).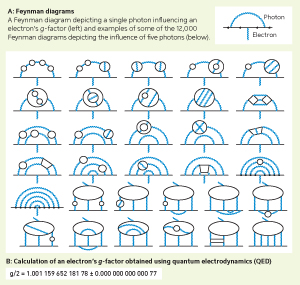

Kinoshita’s team executed the enormous calculations using RIKEN’s supercomputers—then the RIKEN Super Combined Cluster (RSCC), and the RIKEN Integrated Cluster of Clusters (RICC)—over a nine-year period. In 2012, they announced their success in deriving the electron’sg-factor to the precision of 1 part in 1.3 trillion (Fig. 1, part B). To date, this is the most precise theoretical calculation performed in the history of physics.

“Our calculation agreed with Harvard University’s measurement. If it turns out that QED breaks down, there would surely be disagreement between QED-based calculations and the increasingly precise measurements that have been made, but up to now this has not happened,” says Nio. “However, theory predicts that if the precision of experimental measurements is further increased by one digit or so, a disagreement may occur between QED-based calculations and these measurements.”

“Ultimate theories that surpass the current standard theory—including QED—have now been proposed,” continues Nio. “Disagreement between calculated and measured g-factor values will therefore provide an important clue to the determination of which theory is right. Even so, it is quite difficult to increase precision by one digit both experimentally and theoretically.” Hence, Nio is working with Kinoshita to further increase the precision of such calculations to the point where the theories of QED, as established by Tomonaga and others, fail.

Stability of the atomic nucleus

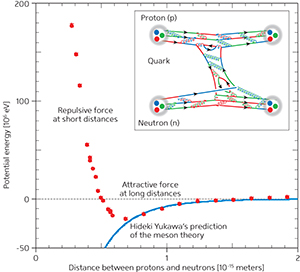
At present, Hatsuda and his colleagues are pushing the boundaries of the research developed by Yukawa. “Atomic nuclei consist of protons and neutrons (Fig. 2, part A). Forces exerted between protons or neutrons are called nuclear forces. In 1935, Yukawa proposed the theory that as protons and neutrons exchange the then-unknown π mesons, an attractive force emerges to form atomic nuclei,” explains Hatsuda.

In the mid-1940s, observations of cosmic rays led to the discovery of the π meson as predicted by Yukawa, verifying his meson theory. “However, a great puzzle remains to be solved with regard to nuclear forces,” Hatsuda notes. “If attractive forces are the only type of nuclear force, the atomic nucleus should collapse because the attraction increases as protons and neutrons approach each other. If so, the current Universe, which is full of galaxies and stars, could not exist stably. Why do atomic nuclei not collapse? This is one of the major enigmas of nuclear physics.”

Later experiments showed that a repulsive force is exerted when protons and neutrons approach each other at distances shorter than a given level, and in the 1960s, they were found to each comprise three particles called quarks (Fig. 2, part A). “To obtain insight into nuclear forces, we must understand the forces exerted between quarks, which are known as ‘the strong interaction’. A theory of the strong interaction was announced by Nambu in 1966,” says Hatsuda.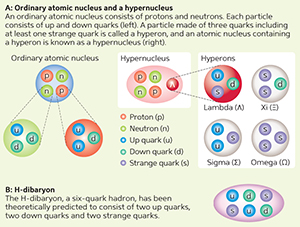

Quantum chromodynamics (QCD), the quantum field theory of elementary particles such as quarks and gluons, was established through the efforts of many researchers across a broad range fields and is able to explain the strong interaction. Experiments in the mid-1970s, established the validity of QCD. “QCD is one of the most beautiful and most complex theories that has been discovered by mankind,” says Hatsuda, enthusiastically.

Successfully calculating nuclear forces

To accurately determine nuclear forces with QCD, enormous calculations are needed. It was therefore necessary to both increase computing speeds and develop a new method of computing. “It was only at the start of the twenty-first century that we became able to accurately calculate the properties of protons and neutrons comprising three quarks using QCD,” says Hatsuda.

In 2005, Hatsuda and his collaborators began to accurately calculate nuclear forces using QCD. The following year, he received the first result from one of his fellow researchers. “The moment I watched it, I felt my body shake because the calculation definitively showed that nuclear forces became not only attractive forces at long distances, but also repulsive forces at short distances (Fig. 3),” he recalls. “I was so excited that I could not help but email many people to inform them of the calculation, including the US physicist Frank Wilczek (the 2004 Nobel Laureate in Physics), who contributed to the establishment of QCD. Wilczek later spoke about our work at the meeting held at Kyoto University in January 2007 to celebrate the centenary of the births of Yukawa and Tomonaga.” 

Hatsuda explains how he was able to obtain accurate calculations of nuclear forces using QCD. “Because I was conducting research into matter at the initial stage of the Universe, I knew a lot about both quarks and atomic nuclei. I was therefore able to mathematically define nuclear forces using QCD. Once defined, the forces could be calculated by large-scale numerical computation.” He and his collaborators performed their calculations with a supercomputer that had just become available at KEK, the High Energy Accelerator Research Organization in Japan.

Entering the next stage using RIKEN’s K computer

Nuclear forces work as repulsive forces over short distances due to the Pauli exclusion principle, a basic principle in quantum physics, says Hatsuda. Particles in the microscopic world can be categorized into one of two types: fermions and bosons. Quarks and electrons are fermions, whereas photons are bosons. Although any number of bosons can occur concurrently at the same position, fermions of the same type cannot—the Pauli exclusion principle.

“There are six types of quark, including up, down and strange,” explains Hatsuda. “Protons and neutrons each comprise a combination of up and down quarks. When protons and neutrons are forced to approach each other within a given distance, up and down quarks in the same state overlap each other at the same position, where repulsive forces work according to the Pauli exclusion principle. The mechanism behind such repulsive forces cannot be elucidated in detail unless the precision of QCD-based computation of nuclear forces is improved.”

To this end, Hatsuda and his colleagues started to calculate nuclear forces using RIKEN’s supercomputer—the K computer—in 2012. “I expect the calculations to be completed in 2014. The answer to the long-asked question of why atomic nuclei do not collapse will finally be found,” he says.

There are now around 3,000 known atomic nuclei. At the RNC, experiments using the Radioactive Isotope Beam Factory (RIBF)—RIKEN’s advanced particle accelerator facility—are being conducted to create a further 4,000 different unstable atomic nuclei, and to examine their properties in detail. The aim is to elucidate the processes by which the atomic nuclei of heavy elements form as a result of supernova explosions.

“Apart from protons and neutrons, each of which consists of up and down quarks only, there are other particles comprising three quarks that include at least one strange quark, known as the hyperons,” notes Hatsuda. “New types of atomic nuclei, known as hypernuclei, are thought to comprise an assembly of hyperons, protons and neutrons (Fig. 2, part A),” he continues. “However, the properties of the nuclear forces of hyperons remain unclear.”

Hatsuda says that researchers at the Japan Proton Accelerator Research Complex (J-PARC), built jointly by KEK and the Japan Atomic Energy Agency, are planning to create many different hypernuclei that contain at least one type of hyperon, such as a lambda (Λ) particle. “Theoretical description of the nuclear forces for hyperons will be essential for advancing the physics of hypernuclei. We aim to carry out such theoretical analysis by accurately calculating the nuclear forces for hyperons from QCD.”

Looking to the future, Hatsuda is planning to focus his research on multi-quark hadrons, which are particles composed of more than four quarks. To date, hadrons comprising two or three quarks have been found, but none of four or more. “Although no definitive evidence has been obtained, it is theoretically possible for such multi-quark hadrons to exist. At J-PARC, researchers are preparing to create a type of hadron—known as the H-dibaryon—comprising six quarks that include two up quarks, two down quarks and two strange quarks (Fig. 2, part B). An important goal of our research is to determine the properties of H-dibaryons through QCD by making accurate calculations with the K computer,” says Hatsuda of the next stage of his team’s research.