PROCESSORS

New insights into phase transitions using artificial intelligence

Researchers from Tokyo Metropolitan University have used machine learning to study spin models, used in physics to study phase transitions. Previous work showed that image/handwriting classifying AI could be applied to distinguish states in the simplest models. The team showed the approach is applicable to more complex models and found that an AI trained on one model and applied to another could reveal key similarities between distinct phases in different systems.

Machine learning and artificial intelligence (AI) are revolutionizing how we live, work, play, and drive. The self-driving car, the algorithm that beat a go grandmaster and advances in finance are just the tip of the iceberg of a wide range of applications which are having a significant impact on society. AI is also making waves in scientific research. A key attraction of these algorithms is how they can be trained with pre-classified data (e.g. images of handwritten letters) and be applied to classify a much wider range of data. {module INSIDE STORY}

In the field of condensed matter physics, recent work by Carrasquilla and Melko (Nature Physics (2017) 13, 431-434) has shown that the same kind of AI used to interpret handwriting, neural networks, could be used to distinguish different phases of matter (e.g. gas, liquid and solid) in simple physical models. They studied the Ising model, the simplest model for the emergence of magnetism in materials. A lattice of atoms with a spin (up or down) has an energy that depends on the relative alignment of adjacent spins. Depending on the conditions, these spins can line up into a ferromagnetic phase (like iron) or assume random directions in a paramagnetic phase. Usually, studies of this kind of system involve analyzing some averaged quantity (e.g. sum of all the spins). The fact that an entire microscopic configuration can be used to classify a phase presented a genuine paradigm shift.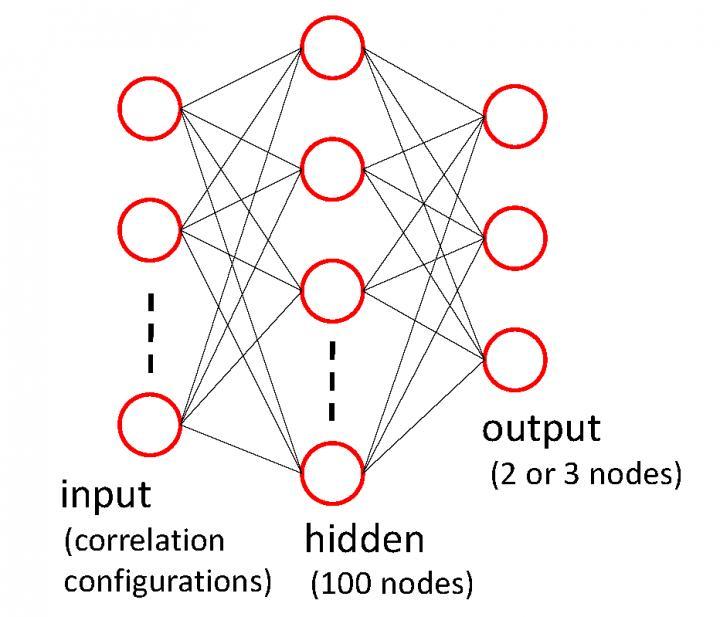 

Now, a team led by Professors Hiroyuki Mori and Yutaka Okabe of Tokyo Metropolitan University are collaborating with the Bioinformatics Institute in Singapore to take this approach to the next level. In its existing form, the method of Carrasquilla and Melko cannot be applied to more complex models than the Ising model. Take the q-state Potts model, where atoms can take one of q states instead of just "up" or "down". Though it also has a phase transition, telling the phases apart is not trivial. In fact, if we consider a 5-state model, there are 120 states which are physically equivalent. To help an AI tell the phases apart, the team gave it more microscopic information, specifically how the state of a particular atom relates to the state of another atom some distance away, or how the spins correlate over the separation. Having trained the AI with many of these correlation configurations for 3 and 5-state Potts models, they found that it was able to correctly classify phases and identify the temperature where the transition took place. They were also able to correctly account for the number of points in their lattice, the finite-size effect. 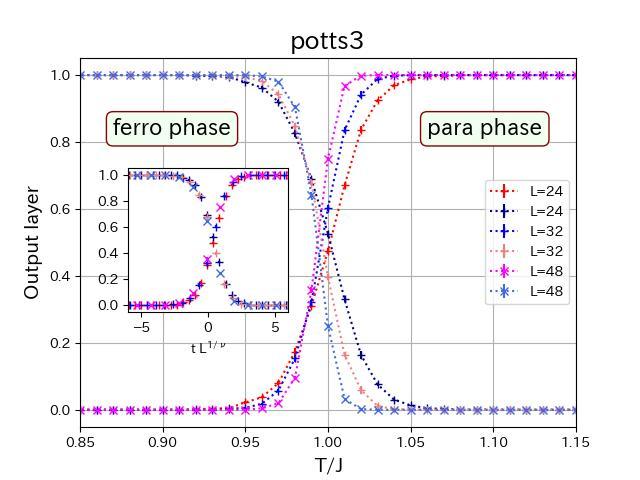{module INSIDE STORY}

Having demonstrated that their method works, they tried the same approach on a q-state clock model, where spins adopt one of q orientations on a circle. When q is greater than or equal to 5, there are three phases which the system can take: an ordered low-temperature phase, a high-temperature phase, and a phase in between known as the Berezinskii-Kosterlitz-Thouless (BKT) phase, the investigation of which won John M. Kosterlitz, David J. Thouless, and Duncan Haldane the 2016 Nobel Prize for Physics. They proceeded to successfully train an AI to tell the three phases apart with a 6-state clock model. When they applied it to configurations from a 4-state clock model, where there are only two phases expected, they discovered that the algorithm could classify the system as being in a BKT phase near the phase transition. This goes to show there is a deep connection between the BKT phase and the critical phase arising at the smooth 'second-order' phase transition point in the 4-state system.

The method presented by the team is generally applicable to a wide range of scientific problems. A key part of physics is universality, identifying traits in seemingly unrelated systems or phenomena which give rise to unified behavior. Machine learning is uniquely placed to tease these features out of the most complex models and systems, letting scientists take a peek at the deep connections that govern nature and our universe.